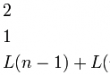প্রজাতি নির্বিশেষে যে কোনো প্রাণী আরেকটি প্রাণীকে সহজেই বন্ধু মনে করার প্রধান শর্ত হলো – প্রাণীটির মস্তিষ্কে নিজের ও অপর প্রাণীটির মধ্যে বৈষম্য বোধের অভাব। এই বৈষম্য বোধের অভাবই উভয়ের মস্তিষ্কের ভাবনার মধ্যে বাঁধন গড়ে তোলে।
Read More »বিজ্ঞানীর সাক্ষাৎকার : স্মার্ট-স্বাস্থ্যসেবার বিজ্ঞানী মাহবুব উল আলম
বিজ্ঞানী ডট অর্গ এর ৭৪ তম সাক্ষাতকারের সিরিজে আমাদের সাথে কথা বলেছেন সুইডেনের প্রবাসী বিজ্ঞানী মাহবু…
সাক্ষাৎকার: পরিবেশ বান্ধব পলিমার বিজ্ঞানী ড. মুহাম্মদ নজরুল ইসলাম
ড. মুহাম্মদ নজরুল ইসলাম চট্রগ্রাম বিশ্ববিদ্যালয়ে রসায়ন বিষয়ে অনার্স ও জৈব রসায়ন বিষয়ে মাস্টার্শ…
সাক্ষাৎকার: হেলথ ইনফরমেটিকস বিশেষজ্ঞ মো. আমিনুল ইসলাম
বিজ্ঞানী ডট অর্গ এর সাক্ষাতকার সিরিজে আমরা কথা বলেছিলাম হেলথ ইনফরমেটিকস বিষয়ের একজন বিশেষজ্ঞ মো. আম…
সাক্ষাতকার: ইন্টারনেট ইঞ্জিনিয়ারিং টাস্ক ফোর্স এর সদস্য এবং গবেষক জাহেদুজ্জামান সরকার
বিজ্ঞানী ডট অর্গ এর সাক্ষাৎকার সিরিজে আমরা এবার মুখোমুখি হয়েছিলাম গবেষক এবং ইন্টারনেট ইঞ্জিনিয়ারিং…
বিজ্ঞানীদের সাক্ষাৎকার #৭২: ড. নিসা খান
বিজ্ঞানী ডট অর্গ এর সাক্ষাৎকার সিরিজের #৭২ তম পর্বে এবার আমাদের মুখোমুখি হয়েছিলেন ড. নিসা খান। ড. ন…
বিজ্ঞানীদের সাক্ষাৎকার #৭০: ড. জুবায়ের শামীম
বিজ্ঞানী ডট অর্গ এর সাক্ষাৎকারের এই ৭০ তম পর্বে এইবার কথা বলেছিলাম ড.জুবায়ের শামীম এর সাথে। ত…
সাক্ষাতকার #৬৯ পর্ব: ড. মাহবুবুর রহমান
বিজ্ঞানী ডট অর্গ এর সাক্ষাৎকার পর্বে আমি কথা বলেছিলাম ড. মাহবুবুর রহমান এর সাথে। তিনি বাংলাদেশের প…
বিজ্ঞানী.ডট.অর্গ এর মুখোমুখি মো.নাজীবুল ইসলাম
বিজ্ঞানী.অর্গ এ আমরা দেশ বিদেশের ছড়িয়ে ছিটিয়ে থাকা বাংলাদেশী বিজ্ঞানীদের সাক্ষাতকার নিয়ে থাকি। আ…
জ্বালানী বিহীন বিশ্ব
বাংলাদেশে আমরা আমাদের প্রয়োজনীয় বিদ্যুতের সমস্যায় সমাধান করতে পারছিনা, তা নিয়ে হিমশিম খেলেও অন্য…
কোডিং শেখার গুরুত্ব ও সম্ভাবনা
ধারণা করা হচ্ছে যে সামনের বিশ্বে কৃত্রিম বুদ্ধিমত্তা দারুণভাবে ভূমিকা রাখবে। সেটা ভালো হবে কি মন্দ হ…
গবেষণা – সমস্যা ও কিছু পথ: অধ্যাপক আতিকুর রহমান আহাদ
মোঃ আতিকুর রহমান আহাদ, অধ্যাপক – ঢাকা বিশ্ববিদ্যালয় এবং বিশেষভাবে নিযুক্ত সহযোগী অধ্যাপক – ওসাকা বি…
২০২১ সনে যে প্রযুক্তিগুলো ভূমিকা রাখবে
নতুন বছরের শুরুতে নতুন করে সব কিছু পর্যালোচনা করে দেখার সুযোগ হয়, তেমনি এই বছরে যে প্রযুক্তিগুলো আল…
আমেরিকায় প্রবাসী ডাক্তার বিজ্ঞানী ডা. মঞ্জুর এর সাথে আলাপন
বিজ্ঞানী.অর্গ এ আমরা দেশ বিদেশে থাকা বিজ্ঞানীদের সাথে বাংলাদেশের পাঠকদের সাথে পরিচয় করে দিই। বিজ্ঞা…
২০২০ সনে যে পাঁচটি প্রযুক্তি মাতাবে বিশ্ব!
নতুন বছরে শুরুতে নতুন করে সব কিছু পর্যালোচনা করে দেখার সুযোগ হয়, তেমনি এই বছরে যে প্রযুক্তিগুলি আলোচ…
প্রোটিনের গঠন পূর্বাভাসে কৃত্রিম বুদ্ধিমত্তা বা এআই মডেলের নতুন সাফল্য
প্রোটিন হচ্ছে জীববিজ্ঞানের অন্যতম গুরুত্বপূর্ণ অণু। এগুলো আমাদের শরীরের প্রতিটি কোষে পাওয়া যায় এবং…
কৃত্রিম বুদ্ধিমত্তা দিয়ে ক্যারিয়ার কাউন্সেলিং কিভাবে নিবেন?
ক্যারিয়ার বিষয়ক কিছু দেখলেই সেটাতে আমার চোখ আটকে যায়। আজকে ফেসবুকে “সিঙ্গাপুর প্রবাসী”…
প্রযুক্তিবিদ প্রকৃতি
হয়ত জেনে আপনি অবাক হবেন যে আমাদের মস্তিষ্ক নতুন যা কিছু ভাবে, সেই ভাবনা আসলে আমাদেরই মস্তিষ্কে থাকা…
কবি ও চ্যাটজিপিটি
লেখক: সৈয়দ শামসুল হক কবিতা লিখি, যেমন আমার অভ্যেস — প্রথমে খাতার পাতায় কলমে, তারপর কম্পিউটারে তাকে…
জাপানে বাংলাদেশি বিজ্ঞানীদের দ্বিতীয় আন্তর্জাতিক কনফারেন্স
বাংলাদেশি বিজ্ঞানীরা শুধু মাত্র দেশের মধ্যেই সীমাবদ্ধ না থেকে ছড়িয়ে পড়ছে বিভিন্ন দেশে এবং বিজ্ঞান…
ব্রডক্লাব কাট্লফিশ্
রীতিমত প্রশিক্ষণ নেওয়ার পরই একজন মানুষ আরেকজন মানুষকে সম্মোহন করার কায়দাটা রপ্ত করতে পারেন। তবে প্রক…
#৬৪ সাক্ষাৎকার: সাইবার সিকিউরিটি বিজ্ঞানী ড. নূরুল মোমেন
বিজ্ঞানী ডট অর্গ এর সাক্ষাৎকারের এই #৬৪ তম পর্বে এইবার কথা বলেছিলাম সাইবার সিকিউরিটি বিষয়ের বিজ্ঞানী…
নতুন সংবাদসমূহ
প্রোটিনের গঠন পূর্বাভাসে কৃত্রিম বুদ্ধিমত্তা বা এআই মডেলের নতুন সাফল্য
প্রোটিন হচ্ছে জীববিজ্ঞানের অন্যতম গুরুত্বপূর্ণ অণু। এগুলো আমাদের শরীরের প্রতিটি কোষে পাওয়া যায় এবং বিভিন্ন …
Read More »কৃত্রিম বুদ্ধিমত্তা দিয়ে ক্যারিয়ার কাউন্সেলিং কিভাবে নিবেন?
ক্যারিয়ার বিষয়ক কিছু দেখলেই সেটাতে আমার চোখ আটকে যায়। আজকে ফেসবুকে “সিঙ্গাপুর প্রবাসী” সিঙ্গাপুর প্রবাসী …
Read More »প্রযুক্তিবিদ প্রকৃতি
হয়ত জেনে আপনি অবাক হবেন যে আমাদের মস্তিষ্ক নতুন যা কিছু ভাবে, সেই ভাবনা আসলে আমাদেরই মস্তিষ্কে থাকা কোন না কোন স্মৃতির এনক্রিপ্টেড্ বা গূঢ়লেখিত রূপ। অন্যভাবে বললে, যে কোন আবিষ্কার বস্তুত আমাদের জানা কোন বিষয়কেই এক নতুন দৃষ্টিভঙ্গিতে দেখা ছাড়া আর কিছুই নয়। যুগ যুগ ধরে মানুষ প্রকৃতির ক্রিয়াকলাপের নানা দিক বিশেষ করে প্রকৃতির সৃষ্টি করা জীব ও তাদের জীবন-ধারণ পর্যবেক্ষণ করছে, সেগুলিকে স্মৃতিবদ্ধ করেছে - প্রকৃতির সাথে এই রসায়নেই মনুষ্য-মস্তিষ্ক হয়েছে গর্ভবতী, প্রসব করেছে প্রযুক্তি !
Read More »কবি ও চ্যাটজিপিটি
লেখক: সৈয়দ শামসুল হক কবিতা লিখি, যেমন আমার অভ্যেস — প্রথমে খাতার পাতায় কলমে, তারপর …
Read More »-
সাক্ষাৎকার : ড. হামিদ
ড. হামিদ একজন বিজনেস ম্যানেজমেন্টের শিক্ষক। বর্তমানে বোস্টনে শিক্ষকতা ও গবেষণার সাথে জড়িত। প্রবাসে থেকেও …
Read More » -
সাক্ষাতকার: ইন্টারনেট ইঞ্জিনিয়ারিং টাস্ক ফোর্স এর সদস্য এবং গবেষক জাহেদুজ্জামান সরকার
-
দেশের জন্য কিছু করতে চাই
-
সাক্ষাৎকার: ড. গোলাম মেজবাহ্ উদ্দিন
-
বিজ্ঞানীর সাক্ষাৎকার : স্মার্ট-স্বাস্থ্যসেবার বিজ্ঞানী মাহবুব উল আলম
-
চিকুনগুনিয়া এর উপর গবেষনা প্রবন্ধ প্রকাশিত হল
চিকুনগুনিয়া অসুখটি বাংলাদেশের স্বাস্থ্যক্ষেত্রে একটি বড় মহামারি এর মতন এসেছিল। কিন্তু ব্যাপারটির উপর বৈজ্ঞানীক ভাবে …
Read More » -
সাবাস ফিরোজ
-
বিশ্বের সবচেয়ে বড় টেলিভিশন
-
কোডিং শেখার গুরুত্ব ও সম্ভাবনা
-
কৃত্রিম বুদ্ধিমত্তা কি মানব জাতির জন্য হুমকি স্বরূপ?
-
গবেষণাপত্র: Increasing homestead Production through Microfinance
ক্রমবর্ধমান জনসংখ্যার প্রবলচাপের ফলে প্রতিবছর ১% করে কৃষি জমি কমছে। আবাসন ব্যবস্থাপনার জন্য উজাড় হচ্ছে …
Read More » -
ব্যাগ গার্ডেনিং
-
‘হুজ হু বাংলাদেশে ২০১৭’ পদক পেয়েছেন প্রফেসর ড ম আ রহিম
-
বাংলাদেশের কৃষক বিজ্ঞানী
-
প্রানী পরিচিতিঃ উড়ন্ত টিকটিকি
-
সূর্য্যের ঘুর্ণন
ছোট বন্ধুরা,তোমরা জান যে পৃথিবী সূর্য্যের চারদিকে ঘোরে আর জান সূর্য্য চুপটি করে দাড়িয়ে দাড়িয়ে …
Read More » -
কিংবদন্তী প্রকৌশলী ও আবিষ্কারক নিকোলা টেসলা
-
বিজ্ঞানী আর্নেস্ট রাদারফোর্ড
-
আবিষ্কারের ইতিকথাঃ ফুয়েল সেল
-
Neptune
-
কম খরচে সিঙ্গেল ব্যাটারি টর্চ
অনেকেই দেখেছেন গ্যাস লাইটারে টর্চ। এই টর্চ গুলো চলে ৩ টি বাটন সেল দিয়ে …
Read More » -
বিভিন্ন ধরনের ব্যাটারি সেল
-
মাইক্রোকন্ট্রোলার দিয়ে সিরিয়াল কমিউনিকেশন সিমুলেশন-পর্ব ১
-
সৌর কোষ কিভাবে কাজ করে?
-
লেড এসিড ব্যাটারি
-
স্টেম সেলের কাছে পরাস্ত হলো এইডস
স্টেম সেল ট্রান্সপ্লান্টের পাঁচ বছর পর এইডস থেকে পুরোপুরি সুস্থ হয়ে উঠেছেন ‘বার্লিন পেশেন্ট’ নামে …
Read More » -
“দ্যা সিক্রেট অফ লাইফ”
-
Coronavirus (কোরোনা ভাইরাস)
-
নিজের শরীরের কোষ থেকেই কান প্রতিস্থাপন করার প্রথম দৃষ্টান্ত দেখাল চীন
-
স্কিতজোফ্রেনিয়া
-
Antibiotic Silk Substrates for Healthcare
লিখেছেন Shafiul Islam Sunday, 12 December 2010 উৎসর্গঃ সৃষ্টির সেবক, রেডিও আবিষ্কারক স্যার জগদীশ চন্দ্র …
Read More » -
Textile and Apparel Workers’ Struggle for Subsistence
-
Coated and Laminated Textiles
-
টেক্সটাইল কলেজ এখন বিশ্ববিদ্যালয়
-
Interfacing Emotion with e-Textiles
-
বিজ্ঞানী ডট কমে বাংলাদেশি বিজ্ঞানী
ইকবাল হোসাইন চৌধুরী প্রকাশিত: প্রথম আলো, ২০০৬ ডিসেম্বর ০১
Read More » -
২০২০ সনে যে পাঁচটি প্রযুক্তি মাতাবে বিশ্ব!
-
তারহীন চার্জার
-
ঈশ্বর কণার পরে ‘ডার্ক ম্যাটারের’ খোঁজ- তারপর?
-
‘পরিধানযোগ্য কম্পিউটার’-ই কী ভবিষ্যৎ?
-
ম্যাজিক স্কয়ার ও রামানুজন
Magic Square হল একটি n×n ম্যাট্রিক্স যার উপাদানগুলো অঋণাত্মক পূর্ণসংখ্যা, যাদের সারি, স্তম্ভ এবং …
Read More » -
লুকাস রাশিমালা
-
বাগান থেকে মহাকাশ – মীজান রহমান
-
গণিতের মূল্য যখন মিলিয়ন ডলার
-
গ্রাফ দিয়ে যায় চেনা
-
Methods and Apparatus for Spinning Spider Silk Protein
উৎসর্গঃ সৃষ্টির সেবক, রেডিও আবিষ্কারক স্যার জগদীশ চন্দ্র বসু – যাঁর স্পর্শে পৃথিবী ধন্য! …
Read More » -
“দ্যা সিক্রেট অফ লাইফ”
-
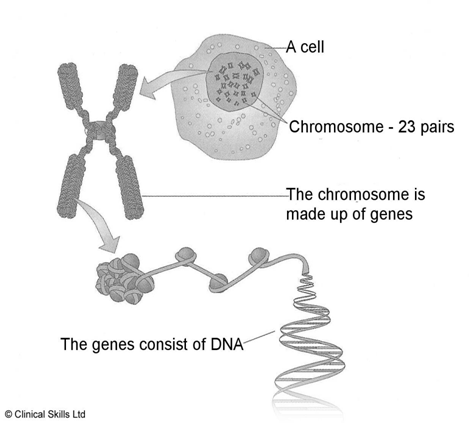
ডি এন এ” কি? প্রথম পর্ব (গঠন)
-
ক্ষতিকর ছত্রাকের জীবনরহস্য উন্মোচন
-
High-toughness Spider Silk Fibers Spun from Soluble Recombinant Silk Produced in Mammalian Cells
-
এডজ কম্পিউটিং (Edge Computing) কি?
ডিভাইসের উপরেই ব্যবহারকারিদের আরো কাছে কম্পিউটিং এবং তথ্য এর প্রোসেস আরো দ্রুত করার অত্যাধুনিক একটি …
Read More » -
২০২০ সনে যে পাঁচটি প্রযুক্তি মাতাবে বিশ্ব!
-
ইউনিভার্সিটি রোভার চ্যালেঞ্জ প্রতিযোগীতায় বাংলাদেশের এমআইএসটি -এর সাফল্য!
-
কৃত্রিম বুদ্ধিমত্তা কি মানব জাতির জন্য হুমকি স্বরূপ?
-
২০২১ সনে যে প্রযুক্তিগুলো ভূমিকা রাখবে
-
পোষাক থেকে শক্তি!
ধরুন, অনেকদিন পর এক পুরনো বন্ধুর ফোন পেয়েছেন। কিন্তু মোবাইলে তখন একফোঁটাও চার্জ নেই। কিংবা …
Read More » -
ন্যানোমেডিসিনে অগ্রগণ্য বিজ্ঞানী ড. মাসুদুর রহমান
-
ন্যানোটেকনোলজী ও কার্বন ন্যানোটিউব
-
গবেষনা: ক্ষুদ্রতম অণুবীক্ষণ যন্ত্র তৈরীর অভিজ্ঞতা
-
ন্যানোপদার্থ এর গবেষক প্রফেসর সাহাব উদ্দিন
-
জ্বালানী বিহীন বিশ্ব
বাংলাদেশে আমরা আমাদের প্রয়োজনীয় বিদ্যুতের সমস্যায় সমাধান করতে পারছিনা, তা নিয়ে হিমশিম খেলেও অন্যদিকে বিশ্বের …
Read More » -
তেজস্ক্রিয়তা ও কুরি দম্পতির কারিকুরি
-
আপেক্ষিক তত্ত্ব(theory of relativity)
-
KEEPING UP WITH TIME
-
Ultra-Violet Radiation (UVR) From Tube Light
-
ethnobotanybd.com এর উদ্দ্যেক্তা সালাহউদ্দিনের সাক্ষাৎকার
গতবছর ethnobotanybd.com সাইটটি দেখে সত্যিই মুগ্ধ হয়েছিলাম। কোন প্রতিদান না চেয়ে, শুধু মাত্র কাজ করার নেশাকে …
Read More » -
উন্নয়নশীল দেশের প্রয়োজন ক্লোনিং প্রযুক্তি
-
বৃহদাকার ডাইনোসর শুধুমাত্র স্বল্প তীক্ষ্ণতা বিশিষ্ট শব্দই শুনতে পেত!
-
Biological weapons as a threat for developing country
-
Methods and Apparatus for Spinning Spider Silk Protein
-
নতুন সাশ্রয়ী সোলার সেল
সম্প্রতি স্ট্যানফোর্ড ইনস্টিটিউট-এর গবেষকরা সূর্যের আলো এবং তাপ একটানা শোষণ করতে পারে এমন একটি পদ্ধতি …
Read More » -
আন্তর্জাতিক ক্ষেত্রে উন্নতমানের গবেষণার স্বীকৃতি পেল ঢাকা বিশ্ববিদ্যালয়
-
অদৃশ্য শক্তির রহস্য উন্মোচনে সুপার-কম্পিউটার
-
ন্যানোমেডিসিনে অগ্রগণ্য বিজ্ঞানী ড. মাসুদুর রহমান
-
দ্বৈত আইনস্টাইন বলয় খুঁজে পেল হাবল মহাকাশ দুরবিন
-
প্রকৃতিবিদ ও বিজ্ঞান লেখক ‘নিসর্গসখা’ দ্বিজেন শর্মা …
শ্রদ্ধাঞ্জলি ~ ‘নিসর্গসখা’ দ্বিজেন শর্মা … PC: Facebook 20170915. Prokashok: সাহিত্য প্রকাশ, February 2015, Price: …
Read More » -
ঝরে গেল আমাদের বড়বৃক্ষ- দ্বিজেন শর্মা
-
সাক্ষাৎকার: ড. তানসীর আলি
-
Meet the Milestone: Dr Amit Chakma, President, UWO
-
ওরালস্যালাইনের (ORS) অন্যতম আবিস্কারক ডা. রফিকুল ইসলাম মারা গেছেন
-
তেজস্ক্রিয়তা ও কুরি দম্পতির কারিকুরি
আবুল বাসার আধুনিক জার্মানি আর চেক রিপাবলিকের সীমান্ত এলাকা। ১৬ শতকের শুরুতে এই অঞ্চলকে দুই …
Read More » -
Methods and Apparatus for Spinning Spider Silk Protein
-
এ মাসের বৈজ্ঞানিক : ড.আবুল হুস্সাম
-
কিভাবে কৃত্রিম হীরা তৈরি করা হয়?
-
বাঁশের আঁশের গবেষণায় নতুন সাফল্য
-
বুদ্ধিমত্তা
বাংলা ভাষায় “মাথা মোটা” কথাটা বুদ্ধিহীন অর্থে ব্যবহৃত হলেও আমরা বৈজ্ঞানিক দৃষ্টিভঙ্গিতে কথাটিকে প্রশংসা হিসাবে …
Read More » -
এম্প্যাথেটিক্ মিরর নিউরন
-
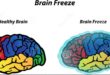
ব্রেইন ফ্রীজ
-
গর্ভবতী মহিলাদের বিড়ালের পরিচর্যা এড়িয়ে চলা উচিত
-
Coronavirus (কোরোনা ভাইরাস)
 বিজ্ঞানী.অর্গ বিজ্ঞানী, প্রযুক্তিবিদ ও পেশাজীবিদের মিলনকেন্দ্র
বিজ্ঞানী.অর্গ বিজ্ঞানী, প্রযুক্তিবিদ ও পেশাজীবিদের মিলনকেন্দ্র